Les étapes pour réussir son exercice de mathématiques

Les exercices de mathématiques peuvent parfois paraître obscurs voire impossibles à résoudre. Pourtant, peu importe la difficulté du problème rencontré, quelques étapes seulement suffisent pour ne pas s’emmêler les pinceaux. Voici donc les cinq étapes essentielles pour être assuré d’avoir toutes les clés en main pour réussir !
Une lecture attentive
Notre première étape est celle de la lecture de l’énoncé. Cette lecture doit être très attentive. Les exercices de mathématiques ont beau être écrits en français, les informations qu’ils contiennent doivent pouvoir être retranscrites en langage mathématique. Il faut donc garder cela en tête en prenant connaissance de l’énoncé.
Exemple d’enoncé classique :
« Aladdin veut se racheter un nouveau tapis volant. Très sentimental il voudrait que son tapis ait exactement la même forme rectangulaire et les même dimensions que l’ancien. Hélas, Aladdin ne se souvient plus des mesures exactes de son tapis. Il se souvient de mémoire que sa largeur faisait 3m et sa diagonale 5m mais comment savoir la longueur du tapis ? »
Le repérage
Notre deuxième étape est celle du repérage. Elle consiste à lister toutes les informations à disposition pour résoudre l’exercice et toutes les informations qui manquent. Enfin, il faut comprendre le but de l’exercice : doit-on faire un calcul, résoudre une équation, démontrer une affirmation ?… Cela permettra tout le long de la réflexion de ne pas perdre de vue l’objectif final.
Quelles sont les informations essentielles de notre énoncé ?
Quelles sont les informations que je connais ? Celles que j’ignore ?
- Mon tapis est un rectangle;
- Sa largeur vaut 3m;
Notons x=3 - Sa diagonale vaut 5m;
Notons y=5 - On ignore la longueur de sa longueur;
Notons-la z
La schématisation du problème
Cette étape n’est pas toujours nécessaire mais pour les exercices portant sur de la géométrie, les vecteurs ou encore les graphiques de fonction, il est parfois utile de se représenter le problème par un petit schéma au brouillon. Cela nous permet de représenter plus clairement ce qui, dans un texte en français, peut paraître plus confus.
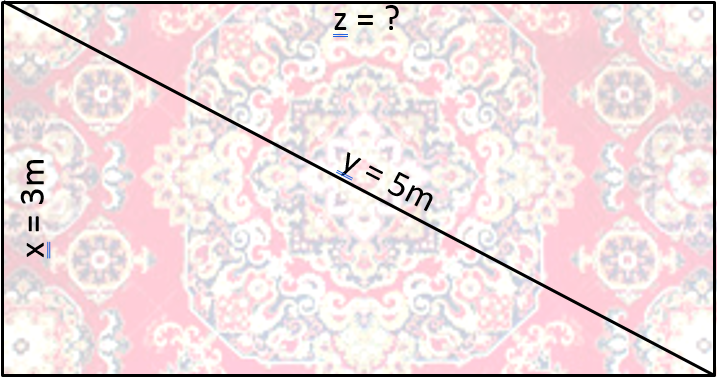
L’algébrisation des données et la résolution du problème
Maintenant que nos données importantes ont été repérées, isolées et éventuellement schématisées il faut les « algébriser ». Concrètement cela signifie qu’il nous faut transformer en langage mathématique ce qui, dans l’énoncé, apparaissait en français.
Ainsi nous pourrons appliquer nos connaissances mathématiques et procéder à la résolution du problème.
Attention ! La rédaction au propre se fait toujours après un premier jet au brouillon.
Transformons notre énoncé en calculs mathématiques :
Pour avoir la longueur il nous suffit d’appliquer le théorème de Pythagore qui nous dit (selon notre propre notation) :
x² + z² = y²
z² = 5² – 3²
z² = 25 – 9
z² = 16
donc z = 4
La longueur du tapis est donc de 4m.
La vérification finale
Avoir trouvé la réponse n’est pas la fin de notre travail ! Il nous faut maintenant effectuer quelques vérifications simples : Avons-nous bien mis les unités correspondantes ? Avons-nous le bon ordre de grandeur ? Avons-nous répondu complètement au problème ? Notre rédaction au propre est-elle claire ?
Cette étape est une étape essentielle dans toutes les matières : tu dois autant l’utiliser en SVT qu’en Histoire ou en Philosophie.
La résolution d’un exercice n’est donc qu’une succession d’étapes élémentaires. En ne perdant jamais de vue ce fil rouge plus aucun problème de maths ne pourra vous paniquer !
